"Progressão" é tudo aquilo que progride, que vai para frente, que muda. Como estamos falando de matemática, certamente será com números. Uma PROGRESSÃO é uma sucessão de números um após o outros (Ex. 1, 1, 2, 3, 5, 8, 13... - ou também, 1, 5, 23, -25, 20, 20, 7,...). Ou seja, quando falamos simplesmente PROGRESSÃO, estamos nos referindo a alguns números colocados um após o outro sem, necessariamente, possuir uma lógica em sua distribuição.
E para ser uma PROGRESSÃO ARITMÉTICA (PA), o que deve acontecer?
Uma progressão aritmética é uma sucessão de números, um após o outro, que seguem um "ritmo definido".
Veja a progressão abaixo:
(1, 3, 5, 7, 9, 11, 13, 15, 17...)
Esta progressão segue um ritmo definido, mostrado na figura abaixo:
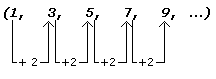
Ou seja, temos um ritmo que é o de SOMAR DUAS UNIDADES a cada elemento que acrescentamos. Este é o ritmo que estamos falando, somar sempre o mesmo número a cada elemento acrescentado.
Como ela é uma progressão numérica que segue um "ritmo definido" de acréscimo em relação ao número anterior, ela pode ser classificada como uma PROGRESSÃO ARITMÉTICA CRESCENTE, pois note que sempre irá crescer.
Veja outro exemplo:
(16, 13, 10, 7, 4, 1, -2, -5...)
Esta também pode ser classificada como uma PA, pois segue um ritmo definido. O qual, diferente da anterior, é de decréscimo. Por ser assim, ela é chamada de PROGRESSÃO ARITMÉTICA DECRESCENTE.
Obs.: Só podemos chamar de P.A. se o ritmo que a seqüência seguir for de acréscimo ou de decréscimo. Se tiver um ritmo diferente não será uma PA. Por exemplo, a seqüência (1, 2, 4, 8, 16, ...) tem um ritmo, sempre dobrar o próximo elemento, mas não é uma PA. :)
Vamos fazer um pequeno exercício agora:
Vamos verificar se as progressões abaixo são P.A., quando for diga se é crescente ou decrescente:
(a) (100, 101, 109, 110, 119, 120...)
(b) (10, 20, 30, 40, 50, 60...)
(c) (-15, -10, -5, 0, 5, 10...)
(d) (1, 2, 3, 4, 5, 6, 7, 8, 9, 10...)
(e) (10, 6, 2, -2, -6...)
(f) (16, 25, 36, 43, 52, 61...)
RESPOSTAS:
(a) Não é uma PA, pois do primeiro para o segundo termo houve um acréscimo de 1 unidade, e do segundo para o terceiro houve um acréscimo de 8 unidades. Para ser PA devemos ter o acréscimo sempre constante.
(b) É uma PA, pois o ritmo se manteve constante do início ao fim. Sempre somando 10, ou seja, CRESCENTE.
(c) É uma PA, pois o ritmo de somar 5 manteve-se constante, ou seja, é uma PA CRESCENTE.
(d) PA CRESCENTE
(e) PA DECRESCENTE
(f) NÃO É PA
Termo Geral
Para um melhor estudo de PA's, vamos agora dar "nome aos bois". Como exemplo, vamos usar a progressão dada anteriormente:
(1, 3, 5, 7, 9, 11, 13, 15, 17...)
O primeiro termo desta PA é 1, o segundo é 3, e assim por diante. Para não desperdiçar lápis e papel, cada termo de uma PA tem seu nome: o primeiro é chamado, normalmente, de a1, o segundo de a2, o terceiro de a3 e assim sucessivamente. Então, nesta PA:
| a1 = 1 a2 = 3 a3 = 5 a4 = 7 ... | O número que aparece no nome do elemento é a "ordem" dele. Ou seja, a1 é oprimeiro, a2 é o segundo, etc. |
Quando temos um termo que não sabemos sua posição, chamamos de an, onde "n" é a posição ocupada pelo termo em questão. Este é o termo geral, pois pode ser qualquer um.
Voltando ao exemplo.
(1, 3, 5, 7, 9, 11, 13, 15, 17...)
Como é uma PA, segue um "ritmo definido" (ritmo este que é a soma de 2 unidades a cada elemento que acrescentamos). Este ritmo também tem um nome: se chama "RAZÃO" e é representada por "r"minúsculo. Portanto, o segundo termo será a soma do primeiro mais a razão; o terceiro será a soma do segundo mais a razão...
Vemos no nosso exemplo que cada próximo termo da progressão é acrescido de 2 unidades, portanto r = 2.
|
| |||||||||||||||||||||||||||||
No quadro 2 acima, vemos que cada termo que aumentamos, colocamos mais uma vez a soma da razão. Vamos rescrever os valores do quadro 2:
QUADRO 2 | ||||||||
| a1 = | 1= a1 |
| ||||||
| a2 = | 1= a1 + r | |||||||
| a3 = | 1= a1 + r + r | |||||||
| a4 = | 1= a1 + r + r + r | |||||||
| a5 = | 1= a1 + r + r + r + r | |||||||
... | ... | |||||||
Note, na coluna destacada, que sempre irá aparecer o primeiro termo (a1) somado com algumas vezes a razão. Há uma relação entre a posição do termo e o número de vezes que a razão aparece (os números grifados em verde no quadro), tente achar esta relação e diga, como seria o termo a22?
Isso mesmo, a22= a1 + 21.r.
Ou seja, se no terceiro termo temos 2 vezes a razão, no quarto termo temos 3, etc. A relação entre tais valores é que o número de vezes que a razão irá aparecer é uma unidade a menos que a ordem do elemento.
Portanto, se quisermos achar o termo de ordem "n" (termo genérico), iremos somar o a1 com (n-1) vezes a razão. Podemos mostrar uma "fórmula" para calcular qualquer termo de uma P.A.:
| an = a1 + (n - 1).r |
Obs.: Uma PA é dita estacionária quando sua razão vale ZERO.
Exercícios:
Qual a razão em cada uma das progressões abaixo?
(A) ( 1, 2, 3, 4, ... )
(B) ( 10, 17, 24, ... )
(C) ( -5, -4, -3, ...)
(D) ( 10, 1, -8, ...)
(E) ( -5, -10, -15, ...)
(F) ( 1/2, 1, 3/2, ...)
(G) ( x, x+2, x+4, ...)
Respostas: |
- Primeiro devemos coletar todas informações do problema: a13 = 5 + (13 - 1).11 |
2) Dados a5 = 100 e r = 10, calcule o primeiro termo:
a5 = a1 + (5 - 1).r |
3) Sendo a7 = 21 e a9 = 27, calcule o valor da razão:
Note que temos duas incógnitas (a1 e r) e duas equações, ou seja, temos um sistema de equações. Vamos isolar o a1 na primeira equação e substituir na segunda: a1 = 21 - 6r Agora, substituindo na segunda: 27 = (21 - 6r) + 8r |
4) (UFRGS) Em uma Progressão Aritmética, em que o primeiro termo é 23 e a razão é -6, a posição ocupada pelo elemento -13 é:
(A) 8a
(B) 7a
(C) 6a
(D) 5a
(E) 4a
- informações do problema: - Substituindo na fórmula do termo geral: |
5) (UCS) O valor de x para que a seqüência (2x, x+1, 3x) seja uma PA é:
(A) 1/2
(B) 2/3
(C) 3
(D) 1/2
(E) 2
- Informações:
- Neste exercício devemos utilizar a propriedade de uma PA qualquer. Sabemos que o termo da frente é igual ao termo de trás mais a razão. Ou seja:
- Como temos "r" igualado nas duas equações, podes igualar uma a outra, ou seja: a2 - a1 = a3 - a2 - Agora, substituindo pelos valores dados no enunciado: (x + 1) - (2x) = (3x) - (x + 1) |
Estas somas são simbolizadas por S25 (soma dos 25 primeiros termos), por S200 (soma dos 200 primeiros termos) ou por Sn (soma dos "n" primeiros termos). Vamos ver um exemplo:
(1, 3, 5, 7, 9, 11, 13, 15, 17, 19)
Esta progressão possui 10 termos, com a1=1, a10=19 er=2. Se quiséssemos saber a soma dos 10 primeiros termos desta PA, poderíamos calcular manualmente, ou seja, 1+3+5+7+9+11+13+15+17+19=100. Mas, se fosse pedido a soma dos 145 primeiros termos?? BAH, manualmente iria demorar muito.
Vamos ver se existe uma maneira mais prática.
Observe quanto vale a soma do primeiro com o último termo desta PA:
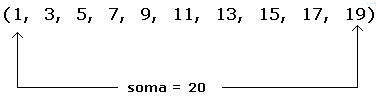
Agora, veja a soma do segundo com o penúltimo:
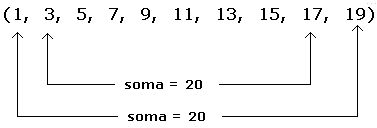
E a soma do terceiro com o antepenúltimo, do quarto com o antes do antepenúltimo ...
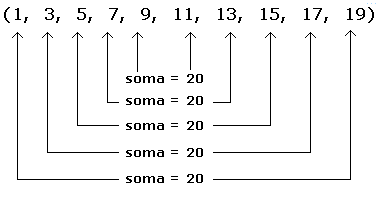
Note, que a soma 20 apareceu exatamente 5 vezes. Ao invés de somar termo a termo, poderíamos somar 5 vezes o 20, ou seja, 5x20=100 (mesmo resultado).
Agora, pense!!! Por que que apareceu cinco vezes a soma = 20?????
Isto mesmo, pois tínhamos 10 termos, e como pegamos eles de 2 em 2, é óbvio que a soma iria aparecer um número de vezes igual a metade do número de termos!
E agora, se fosse uma progressão com 100 elementos? Deveríamos proceder da mesma maneira!
A soma do primeiro com o último iria se repetir por 50 vezes (metade de 100), portanto, matematicamente falando teríamos:
S100=(a1+a100).50
Para concluir. Se tivéssemos que calcular a soma dos elementos de uma PA com "n" termos? A soma do primeiro com o último iria se repetir por n/2 vezes. Ou seja, podemos escrever:
Dê uma olhada nos exercícios abaixo e veja como é fácil:
1) O primeiro termo de uma PA é 100 e o trigésimo é 187. Qual a soma dos trinta primeiros termos?
- Informações do problema: - Aplicando a fórmula da soma, temos: |
2) Sabendo que o primeiro termo de uma PA vale 21 e a razão é 7, calcule a soma dos 12 primeiros termos desta PA:
- Informações do problema: - Colocando na fórmula da soma, vemos que está faltando um dado. Qual o valor de a12? Então antes de tudo devemos calcular o valor de a12. - Agora sim, podemos colocar na fórmula da soma: |
3) A soma dos n primeiros termos de uma PA é dada por Sn=n2+2n. O valor do 13o termo desta PA é:
(A) 195
(B) 190
(C) 27
(D) 26
(E) 25
- Este tipo de questão é clássica, pois tem um pega ratão horrível. Então, vamos esmigalhar ao máximo. Te liga só! - À primeira vista você pode achar que se substituirmos "n" por 13 teremos o valor do 13o termo. Aí está o pega ratão, substitua e veja a resposta da letra "A" (pega ratão). - Agora tem que se ligar. S2 significa a soma de todos os termos até a2, então é igual à a1+a2. Como já sabemos o valor de a1,logo: Se a1=3 e a2=5 a razão só pode ser 2. Agora podemos achar o 13o termo, é só substituir na fórmula do termo geral:
|
Este tópico nada mais é do que uma simples interpretação do que é pedido no exercício.
Primeiramente devemos saber o que significa o verbo "interpolar". Significa "colocar entre".
E, "meios artméticos", significa "números que formam uma PA". Veja os exercícios resolvidos:
1) Interpolando 10 meios aritméticos entre 5 e 38, teremos uma PA de razão: (A) 1 |
- Interpretando o que é dito: o exercício pede para colocarmos 10 números entre 5 e 38. Assim, teremos:
- Como inserimos dez termos no meio dos dois já existentes, a PA terá, 12 termos. Então, as informações deste exercício são: a1=5 e a12=38 r=? - Agora é só usar a fórmula do termo geral : |
2) Quantos meios devemos interpolar entre 112 e 250 para termos uma PA de razão 23?
(A) 3
(B) 4
(C) 5
(D) 6
(E) 7
- Informações do problema: - Devemos utilizar a fórmula do termo geral de uma PA: - Aqui que a cobra fuma, meu amigo. A alternativa "E" tá te esperando, pedindo pra tu marcá-la. 7 não é a resposta, é o número total de termos. Devemos retirar desta contagem os termos 112 e 250, pois é pedido quantos termos devem ser inseridos "ENTRE" estes dois. Portanto, se no total temos 7 termos, excluindo dois da contagem, temos 5 termos para inserir entre o 112 e o 250. A resposta certa é a letra "C" |
1) O sétimo termo de uma PA é 20 e o décimo é 32. Então o vigésimo termo é
(A) 60
(B) 59
(C) 72
(D) 80
(E) 76
2) O único valor de x que verifica a equação (x-2)+(x-5)+(x-8)+...+(x-47)=424 é
(A) 51
(B) 41
(C) 31
(D) 61
(E) 71
3) (PUC-RS) Na seqüencia definida por , a soma dos 10 primeiros termos é igual a
(A)
(B)
(C) 53
(D) 265
(E) 530
4) (UFRGS) Os números que exprimem o lado, a altura e a área de um triângulo equilátero estão em PA, nessa ordem. A altura desse triângulo mede
(A)
(B)
(C)
(D)
(E)
5) (UFRGS) A PA (a1, a2, a3, ...) tem razão "r". A razão da progressão definida por bn=a5n é
(A) r
(B) r+r
(C) 5r
(D) r-5
(E) r/5
6) (ULBRA) O número de termos de uma PA, cuja razão é 9, o primeiro termo é 4 e o último 58, é
(A) 3
(B) 4
(C) 5
(D) 6
(E) 7
7) A soma dos 40 primeiros números naturais é igual a
(A) 400
(B) 410
(C) 670
(D) 780
(E) 800
8) (UFCE) Um atleta corre sempre 400 metros a mais que no dia anterior. Ao final de 11 dias ele percorre um total de 35200 metros. O número de metros que ele correu no último dia foi igual a
(A) 5100
(B) 5200
(C) 5300
(D) 5400
(E) 5500
9) (PUC) A soma dos n primeiros termos de uma PA é dada por Sn=3n2+5n. a razão dessa PA é:
(A) 7
(B) 6
(C) 9
(D) 8
(E) 10
10) (UFRGS) Para p e q inteiros positivos, a soma dos cem primeiros múltiplos de p é A e a soma dos cem primeiros múltiplos de q é B. O valor de A+B é
(A) 200pq
(B) 200(p + q)
(C) 500(p + q)
(D) 5050(p + q)
(E) 5050pq
11) (PUC) A quantidade de meios aritméticos que se devem interpolar entre -a e 20a, a fim de se obter uma PA de razão 7, é
(A) 3a-2
(B) 3a-1
(C) 3a
(D) 3a+1
(E) 3a+2
12) (FUVEST) Do conjunto de todos os números naturais n, n ≤ 200, retiram-se os múltiplos de 5 e, em seguida, os mútiplos de 6. Calcule a soma dos números que permanecem no conjunto.
13) (UFSM) Tisiu ficou sem parceiro para jogar bolita (bola de gude); então pegou sua coleção de bolitas e formou uma seqüência de "T" (a inicial de seu nome), conforme a figura

Supondo que o guri conseguiu formar 10 "T" completos, pode-se, seguindo o padrão, afirmar que ele possía
(A) mais de 300 bolitas.
(B) pelo menos 230 bolitas.
(C) menos de 220 bolitas.
(D) exatamente 300 bolitas.
(E) exatamente 41 bolitas.
(A) 60
(B) 59
(C) 72
(D) 80
(E) 76
- Informações do problema: - Primeiro vamos colocar todos termos conhecidos na fórmula do termo geral: - Formamos um sistema de equações e resolvemos:
|
2) O único valor de x que verifica a equação (x-2)+(x-5)+(x-8)+...+(x-47)=424 é
(A) 51
(B) 41
(C) 31
(D) 61
(E) 71
- Note que temos uma PA no lado esquerdo da equação com: - Sabemos que é uma PA pois a cada termo estamos somando uma mesma constante (a razão, que no caso é -3). Para descobrir esta razão simplesmente fazemos:
- Como os termos estão sendo somados, devemos usar a fórmula da soma dos termos de uma PA. Já sabemos o primeiro termo, o último termo e a razão, mas para usar a fórmula da soma devemos saber o número de termos (ou seja, "n"). Para calcularmos vamos aplicar a fórmula do termo geral no último termo: an=a1+(n-1)r Substituindo por seus valores - Agora sim podemos usar a fórmula da soma: - Vamos voltar na equação do exercício e substituir todo lado esquerdo da equação pelo valor calculado: |
3) (PUC-RS) Na seqüencia definida por , a soma dos 10 primeiros termos é igual a
(A)
(B)
(C) 53
(D) 265
(E) 53
- O exercício dá a fórmula do termo geral de uma PA e pede S10. Utilizaremos a fórmula da soma, mas para usá-la devemos saber a1e a10. Estes valores iremos calcular com a fórmula dada pelo exercício: - Agora é só aplicar a fórmula da soma: Resposta certa, letra "B". |
4) (UFRGS) Os números que exprimem o lado, a altura e a área de um triângulo equilátero estão em PA, nessa ordem. A altura desse triângulo mede
(A)
(B)
(C)
(D)
(E)
- Para resolver este exercício devemos ter um conhecimento de Geometria Plana. Este capítulo iremos estudar mais adiante. Mas vamos chamar o lado do triângulo de "L", a fórmula da altura de um triângulo equilátero é - O problema pede o valor da altura, e para isso devemos antes achar o valor de L. Vamos utilizar a propriedade fundamental de uma PA: Chegamos em uma equação incompleta do segundo grau. Para facilitar os cálculos, coloquei o L em evidência. Agora é só calcular as raízes, no caso são O exercício pede a altura do triângulo, vamos aplicar a fórmula da altura (h): Nas resposta o problema coloca o 2 em evidência, assim sendo: Resposta certa, letra "C". |
5) (UFRGS) A PA tem razão
. A razão da progressão definida por
é
(A)
(B)
(C)
(D)
(E)
- Para calcularmos a razão da segunda PA devemos saber no mínimo dois termos em sequência desta PA. Vamos então calcular o primeiro e o segundo.
Agora que já sabemos que b1=a5 e b2=a10 vamos ver quanto vale a5 e a10 :
Para calcularmos a razão da PA "b" (vamos chamar de R maiúsculo) é só calcularmos b2-b1 : |
6) (ULBRA) O número de termos de uma PA, cuja razão é 9, o primeiro termo é 4 e o último 58, é
(A) 3
(B) 4
(C) 5
(D) 6
(E) 7
- Informações: - Vamos somente aplicar a fórmula do termo geral: |
7) A soma dos 40 primeiros números naturais é igual a
(A) 400
(B) 410
(C) 670
(D) 780
(E) 800
- Podemos olhar para os números naturais como uma PA com a1=0 e r=1. - Aqui tem um pega ratão! Para usar a fórmula da soma devemos saber que é o a40. Você pode achar que é o 40, mas não. Vamos calcular! - Viu! Agora vamos aplicar a fórmula da soma. |
8) (UFCE) Um atleta corre sempre 400 metros a mais que no dia anterior. Ao final de 11 dias ele percorre um total de 35200 metros. O número de metros que ele correu no último dia foi igual a
(A) 5100
(B) 5200
(C) 5300
(D) 5400
(E) 5500
- Informações: - Neste exercício iremos usar a fórmula da soma dos termos, mas para isso devemos calcular o valor de an em função de a1 e r. Calma lá, veja só: - Agora sim vamos colocar na fórmula da soma: - Calculamos o valor de a1, agora é só substituir na fórmula de a11 para achar seu valor (pois é isso que o problema quer, o valor do último dia): |
9) (PUC) A soma dos n primeiros termos de uma PA é dada por Sn=3n2+5n. a razão dessa PA é:
(A) 7
(B) 6
(C) 9
(D) 8
(E) 10
- Esta questão é clássica! Tem um pega-ratão tenebroso. O problema dá a fórmula geral da soma dos n primeiros termos de uma PA. Vamos substituir valores e achar os dois primeiros termos para calcularmos a razão (que é o que o problema pede). - Se substituirmos o "n" por 1 teremos S1 que equivale dizer "a soma dos 1 primeiros termos", ou seja, o próprio primeiro termo. - Agora que tem o pega-ratão! Se substituirmo "n" por 2 teremos a soma dos 2 primeiros termos, ou seja, a1+a2: - Lembre-se que este é o valor de a1+a2 portanto: - Para achar o valor da razão, fazemos a2-a1: |
10) (UFRGS) Para p e q inteiros positivos, a soma dos cem primeiros múltiplos de p é A e a soma dos cem primeiros múltiplos de q é B. O valor de A+B é
(A) 200pq
(B) 200(p + q)
(C) 500(p + q)
(D) 5050(p + q)
(E) 5050pq
- Sabemos que os múltiplos de um número "n" seguem conforme uma PA de razão r=n e a1=n. Exemplo, os múltiplos de 5: {5, 10, 15, 20, 25, 30, 35, 40, 45, 50...} - Então para os múltiplos de "p" temos uma PA com r=p e a1=p. O problema diz que "A" é a soma dos 100 primeiro múltiplos de "p". Podemos aplicar a fórmula da soma dos termos de uma PA, mas para isso devemos saber o valor de a100, vamos calculá-lo aplicando a fórmula do termo geral: - Agora podemos calcula a soma dos cem primeiros, ou seja, o valor de "A". - Com este mesmo raciocínio vamos calcular "B". - Concluímos que o valor de A+B é 5050p+5050q, colocando o 5050 em evidência, temos: |
11) (PUC) A quantidade de meios aritméticos que se devem interpolar entre -a e 20a, a fim de se obter uma PA de razão 7, é
(A) 3a-2
(B) 3a-1
(C) 3a
(D) 3a+1
(E) 3a+2
- Informações: - Vamos utilizar a fórmula do termo geral: Agora não caia no pega-ratão, acabamos de calcular o número de termos que deve ter a progressão. O exercício pede quantos devem ser INSERIDOS entre -a e 20a, portanto devemos diminuir duas unidades: 3a+1-2 |
Recomendamos: http://www.tutorbrasil.com.br/



qq isso ein glr? tao mandando ver no blog!
ResponderExcluirass rodrigo rodrigues do pré vest =p
4:50 AM OASHEOSIEASOI
E ai rodrigo blz?
ResponderExcluirvlw por reconhecer nosso trabalho!!
Continue conferindo as outras postagens do nosso blog!
abç brother!!
Equipe Pre Vestibular Online.
Maravilhoso aki...continuem assim,vcs naum sabem o tanto que estão me ajudando...e com certeza terão um peso enorme na minha aprovação no vestibular -ENEM ;]
ResponderExcluir=D
cade a resoluçao do 13???????????????? sacanagem
ResponderExcluirMinha 13 deu 41 bolinhas '-'
ResponderExcluir