Geometria Poliedros

O estudo da geometria está diretamente ligado com as formas da natureza e o estudo da geometria de posição é essencial para a compreensão da geometria espacial.

Dentro da geometria de posição são estudados conteúdos como:

• Posição de retas e pontos no espaço e no plano.
• Ângulos formados entre: planos e retas, somente entre retas, somente entre planos,

Que são necessários para a formação de poliedros no espaço.

Nessa seção você irá encontrar informações sobre todos os tipos de sólidos e suas respectivas características, como construí-los e representá-los no espaço. O estudo sobre poliedros e corpos redondos receberá maior ênfase na identificação de seus elementos, no cálculo da suas áreas e volumes, pois são sólidos geométricos de fácil identificação no nosso dia-a-dia.

Poliedros são sólidos geométricos ou figuras geométricas espaciais formadas por três elementos básicos: faces, arestas e vértices.

Os Poliedros podem ser convexos e não convexos.

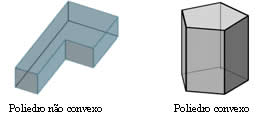
Ao estudarmos os poliedros convexos verificamos uma importante relação existente entre o número de faces, arestas e vértices. Leonhard Euler foi um matemático suíço que, dentre várias contribuições para a Matemática, desenvolveu uma relação que calcula o número de arestas (A), faces (F) e vértices (V) de um poliedro, desde que haja dois valores.

Relação de Euler: V – A + F = 2 ou V + F = A + 2

Exemplo 1
Calcule o número de arestas de um sólido que possui 8 vértices e 6 faces.

V – A + F = 2
8 – A + 6 = 2
A = 14 – 2
A = 12

Exemplo 2
Um sólido geométrico tem 6 vértices e 10 arestas. Calcule o número de faces desse sólido.

V – A + F = 2
6 – 10 + F = 2
F = 2 + 4
F = 6

Poliedros de Platão
Todo poliedro considerado de Platão deve obedecer algumas condições:

O número de arestas tem que ser igual ao número de faces.
Os ângulos do poliedro devem possuir o mesmo número de arestas.
A equação de Euler precisa ser aplicada e aceita.

Poliedros regulares
Todas as faces iguais e regulares
Os ângulos poliédricos precisam possuir o mesmo valor.

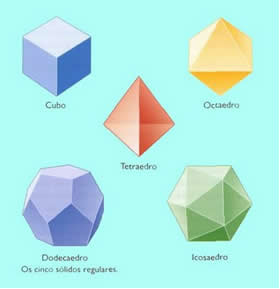
Temos a certeza da existência de cinco poliedros regulares, os chamados poliedros de Platão: tetraedro, hexaedro ou cubo, dodecaedro, octaedro e icosaedro.

COMPARTILHAR:

Curtir

+1

Tweet

Tweet